As it has been given that
 ,
,
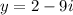 .
.
We need to find the value of the following:
(i)
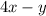 , substituting the value of 'x' and 'y' in the expression, we get:
, substituting the value of 'x' and 'y' in the expression, we get:
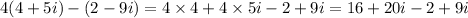
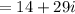
So,
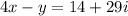
(ii)
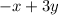 , substituting the value of 'x' and 'y' in the expression, we get:
, substituting the value of 'x' and 'y' in the expression, we get:
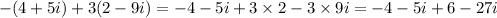

So,
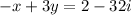
(iii)
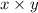 , we need to substitute the value of 'x' and 'y' in the expression, for this, we can use distributive property of multiplication that says,
, we need to substitute the value of 'x' and 'y' in the expression, for this, we can use distributive property of multiplication that says,
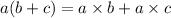
Using the distributive property of multiplication:
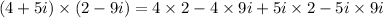

Now, we know that

We get,
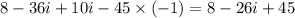
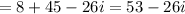
Therefore,
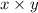 =
=
 .
.
(iv) We have,
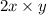 , we need to substitute the value of 'x' and 'y' in the expression, we get:
, we need to substitute the value of 'x' and 'y' in the expression, we get:

Again, we can use distributive property of multiplication that says,
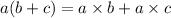
So,
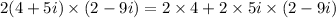

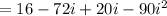
since,
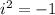
we get,
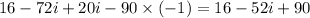
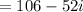
Therefore,
