Question

A box of candy hearts contains 52 hearts, of which 19 are white, 10 are tan, 7 are pink, 3 are purple, 5 are yellow, 2 are orange, and 6 are green. if you select 9 pieces of candy randomly from the box, without replacement, give the probability that

a.three of the hearts are white.
b.three are white, 2 are tan, 1 is pink, 1 is yellow, and 2 are green.

Answer 1

a. Probability that three of the candies are white = 0.29

b. Probability that three are white, 2 are tan, 1 is pink, 1 is yellow, and 2 are green = 0.006

Solution-

There are 19 white candies, out off which we have to choose 3.

The number of ways we can do the same process =

`\binom{19}{3} = (19!)/(3!16!) = 969`

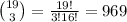
As we have to draw total of 9 candies, after 3 white candies we left with 9-3 = 6, candies. And those 6 candies have to be selected from 52-19 = 33 candies, (as we are drawing candies other than white, so it is subtracted)

And this process can be done in,

`\binom{33}{6} = (33!)/(6!27!) =1107568`

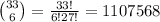
So total number of selection = (969)×(1107568) = 1073233392

Drawing 9 candies out of 52 candies,

`\binom{52}{9} = (52!)/(9!43!) = 3679075400`

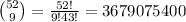
∴P(3 white candies) =
`(1073233392)/(3679075400) =0.29`

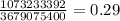
Total number of ways of selecting 3 whites, 2 are tans, 1 is pink, 1 is yellow, and 2 are greens is,

`\binom{19}{3} \binom{10}{2} \binom{7}{1} \binom{5}{1} \binom{6}{2}`

`=((19!)/(3!16!)) ((10!)/(2!8!)) ((7!)/(1!6)) ((5!)/(1!4!)) ((6!)/(2!4!))`

`=(969)(45)(7)(5)(15)=22892625`

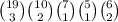
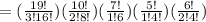
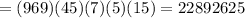
Total number of selection = 3 whites + 2 are tans + 1 is pink + 1 is yellow + 2 greens = 9 candies out of 52 candies is,

`\binom{52}{9}=(52!)/(9!43!) =3679075400`

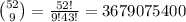
∴ P( 3 whites, 2 are tans, 1 is pink, 1 is yellow, 2 greens) =

`(22892625)/(3679075400) = 0.006`