Question

What is the stopping distance if the car is initially traveling at speed 5.0v? assume that the acceleration due to the braking is the same in both cases?

Answer 1

The question seems to be expecting a comparative answer.

Let us consider Scenario 1 first.

We have the variables listed as follows:

Initial Velocity
`V_(i)` = v m/s

Final Velocity
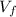`V_(f)` = 0, since the car is stopping.

Acceleration = - a
`m/s^(2)` , since the car is slowing down.

Let the stopping distance in this case be S

We can arrive at the expression for S by using the equation
`V_(f)^(2) } = V_(i)^(2) } + 2aS`

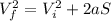
Plugging in what we know, we get
`0 = v^(2) - 2aS`

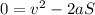
Hence, stopping distance in Scenario 1 is
`S = (v^(2) )/(2a)`

Now, considering Scenario 2, we have

Initial Velocity
`V_(i)` = 5v m/s

Final Velocity
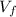`V_(f)` = 0

Acceleration = - a
`m/s^(2)`, since it is given to be same in both the cases.

Let the stopping distance this time be
`S_(2)`

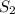
We can use the same equation for this scenario too, i.e.
`V_(f)^(2) } = V_(i)^(2) } + 2aS`

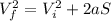
Plugging in what we have, we get
`0 = (5v)^(2)  - 2aS_(2)`

Solving this for
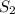`S_(2)`, we get
`S_(2)  = 25. (v^(2) )/(2a)`

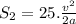
This can be written in terms of S as
`S_(2) = 25.S`

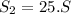
Thus, the car's new stopping distance will be 25 times compared to the older one!