Question

find two numbers such that the smaller subtracted from the larger is 9 and the difference of the square of the larger subtracted from square of the smaller is 9

Answer 1

GIVEN - The subtraction of the smaller number from the larger number be 9.

The subtraction of the square of the smaller number from the square larger number be 9.

Find the number

to proof =

let larger number be x

and let the smaller number be y

`x - y =9`

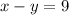
and the second equation becomes

`x^(2) -y^(2) = 9`

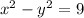
by using the equation

we have

`x^(2) -y^(2)` = (x - y) (x +y)

now put this in the above equation we get

thus we have

(x-y) (x+y) = 9

as we have (x-y) =9

put in the above equation

we get

(x + y ) =1

by solving the equation (x + y ) = 1 & (x - y) = 9

we get x = 5 & y = -4

Hence proved

Answer 2

Answer: The numbers are 5 and (-) 4

Explanation:

Let the larger number be x

Let the smaller number be y

According to question,

`x-y=9` ---- equation (1)

and

`x^2-y^2=9` --- equation (2)

Now, we use the equation (2)

`(x-y)(x+y)=9\\9 * (x+y)=9\\(x+y)= (9)/(9)\\x+y=1`

So, the only possible number can x = 5 and y = (-) 4

as it satisfies both the equations.