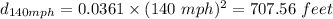Question

According to car and driver, an alfa romeo going at 70 mph requires 177 feet to stop. assuming that the stopping distance is proportional to the square of the velocity, find the stopping distances required by an alfa romeo going at 60 mph and at 140 mph (its top speed). (round your answers to two decimal places.)

Answer 1

Let d represents the stopping distance required by an alfa romeo.

The stopping distance is proportional to the square of velocity is equivalent to the equation,

`d=kv^2`

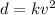
Here, k is proportionality constant.

Given, d = 177 feet and v = 70 mph.

So, proportionality constant

`k=(177\ feet )/((70\ mph)^2) \simeq 0.0361`.

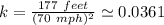Thus, the stopping distances required by an alfa romeo going at 60 mph and at 140 mph,

`d_(60mph) =0.0361 * (60\ mph)^2 =129.96\ feet`

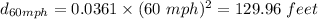
and

`d_(140mph) =0.0361 * (140\ mph)^2 =707.56\ feet`