Question

The difference of the squares of two positive consecutive even integers is 4444. find the integers. use the fact​ that, if x represents an even​ integer, then xplus+2 represents the next consecutive even integer.

Answer 1

Remember that the formula for the difference of squares is
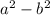`a^2 - b^2`, where
`a` and
`b` are expressions or values.

In this case, we have two expressions,
`x` and
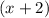`(x + 2)`. We are also given that their difference of squares is 4444. Using the formula, we can say:

`(x + 2)^2 - x^2 = 4444`

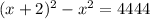
Now, we can solve for
`x`:

`(x + 2)^2 - x^2 = 4444`

`(x^2 + 4x + 4) - x^2 = 4444`

`4x + 4 = 4444`

`4x = 4440`

`x = 1110`

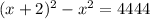
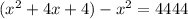
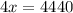
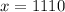
We now know that the first number is 1110. To find the second number, we must add 2 to the first number, which means that the second number, represented by
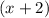`(x + 2)`, is equal to 1112.

Our two numbers are 1110 and 1112.