Question

How do you solve this equation x^1/4+1=0?

Answer 1

First, let's isolate
`x` on one side of the equation. To do this, we can subtract 1 from both sides of the equation:

`x^{(1)/(4)} = -1`

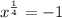
Now, we are going to want to get x to a power of 1, since that is what we are looking for after all. To do this, we can set both sides of the equation to the exponent of 4:

`(x^{(1)/(4)})^4 = (-1)^4`

`x = 1`

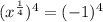
We have found x = 1. However, let's check this answer to make sure that it is not an extraneous solution:

`1^{(1)/(4)} \stackrel{?}{=} -1`

`1^{(1)/(4)} = 1 \\eq -1`

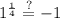
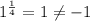
When we substitute x = 1 into the original equation, we get 1, which is not -1. Thus x = 1 is an extraneous solution. Since there are no other values that we found, the equation has no solutions.