Answer with explanation:
Equation of line passing through two points ,

Equation of line passing through the points (4, 5) and (10, 2) is
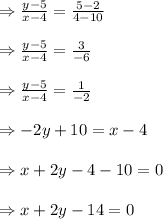
To Find the inverse of the function obtained below
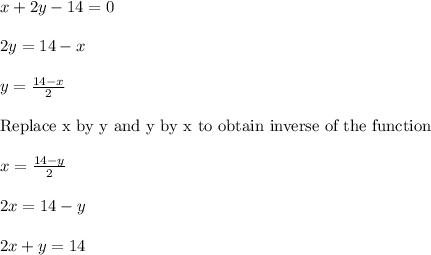
⇒⇒The equation
2 x + y=14
represents an inverse variation function that passes through the points (4, 5) and (10, 2).