Solution: (1)The interval notation of
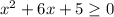 is
is
![(-\infty ,5]\cup [-1,\infty )](https://img.qammunity.org/2019/formulas/mathematics/high-school/vpslx9wehm3mjgdc6k52hs9lyqlappupxg.png) .
.
Step-by-step explanation:
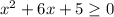
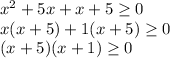
The product of two expression is positive if and only if both are positive or both are negative.
case 1:
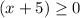 and
and

Then
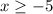 and
and

From above conditions
 .
.
case 2:
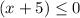 and case 2:
and case 2:
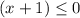
Then
 and
and

From above conditions
 .
.
By case 1 and 2 it is conclude that the interval notation of
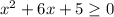 is
is
![(-\infty ,5]\cup [-1,\infty )](https://img.qammunity.org/2019/formulas/mathematics/high-school/vpslx9wehm3mjgdc6k52hs9lyqlappupxg.png) .
.
Solution: (2) The interval notation of
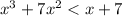 is
is
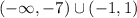 .
.
Step-by-step explanation:
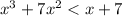
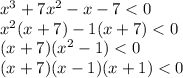
The relative equation of the above inequality is

Equate each factor equal to 0. The zeros of above equation is -7,-1 and 1. These points divides the number line in 4 parts or intervals. The any value from those interval to check the inequality. If the test point satisfies the equality then that interval is the solution of the inequality.
By the above process the interval notation of
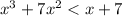 is
is
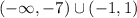 .
.
Solution: (3) The ball is lower than the building for
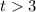 .
.
Step-by-step explanation:
The height of the ball is given by the equation
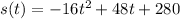 and the height of the building is 280ft.
and the height of the building is 280ft.
The ball is lower than the building if the height of the ball is less than 280ft, i.e.,
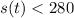 .
.
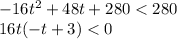
The time is always positive, so the first factor 16t is always positive. Since first factor is positive and the product of both factors is less than zero, therefore the second factor (-t+3) is always less than zero.
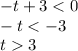
Therefore, the ball is lower than the building for
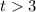 .
.