Answer:
D. 3.5
Explanation:
In order to find the answer we can use the distance equation as follows:

Notice that points P(2,4) and A(2,4) have the same coordinates, so we need to calculate the distances PQ and PR and compare them respectively to AB and AC, so:
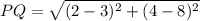
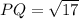
and
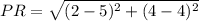
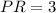
Now,
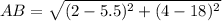
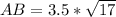
and
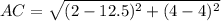
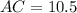
Now let's find the ratios:
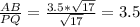
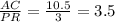
In conclusion, the scale factor of the dilation is 3.5, so the answer is D.