Question

Solve 5x-4 = |2x+1|. Check for extraneous solutions.

Answer 1

So firstly, we have to break down this equation into two since it's an absolute value equation. Break down the equation as such:
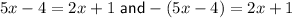`5x-4=2x+1\ \textsf{and}-(5x-4)=2x+1` . Let's start with the first equation:

Firstly, subtract 2x on both sides of the equation:
`3x-4=1`

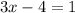
Next, add 4 on both sides:
`3x=5`

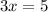
Lastly, divide both sides by 3 and your first answer will be
`x=(5)/(3)`

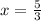
Next, let's solve the other equation. Firstly, distribute the minus sign to (5x - 4) (think of the minus sign as -1):
`-5x+4=2x+1`

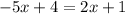
Next, add 5x to both sides:
`4=7x+1`

Next, subtract 1 on both sides:
`3=7x`

Lastly, divide both sides by 7 and your second answer will be
`(3)/(7)=x`

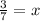
Now, an extraneous solution is a solution that is found in the equation, but does not hold true when plugged back into the equation. To check if either of our solutions are extraneous, plug them back into the original equation and solve:

Starting with 5/3, firstly plug the value back into the equation:

`5* (5)/(3)-4=|2* (5)/(3)+1|`

Next, solve the multiplication:

`(25)/(3)-4=|(10)/(3)+1|`

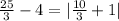
Next, to be able to solve the addition (10/3 + 1/1) and subtraction (25/3 - 4/1), we need to find the LCD, or lowest common denominator, of 3 and 1. To find the LCD, list the multiples of the two and the lowest one they share is their LCD. In this case, their LCD is 3. Multiply both sides of 1/1 and -4/1 by 3/3:

`(1)/(1)* (3)/(3)=(3)/(3)\\\\-(4)/(1)* (3)/(3)=-(12)/(3)\\\\(25)/(3)-(12)/(3)=|(10)/(3)+(3)/(3)|`

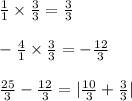
Next, solve the addition and subtraction:

`(13)/(3)=(13)/(3)`

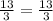
Now since 13/3 = 13/3 is true, this means that 5/3 is a non-extraneous solution.

Now, let's plug in our other solution 3/7 into the equation:

`5* (3)/(7)-4=|2* (3)/(7)+1|`

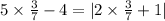
Firstly, solve the multiplications:

`(15)/(7)-4=|(6)/(7)+1|`

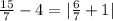
Next, find the LCD of 1 and 7. In this case, it's 7. Multiply both sides of -4/1 and 1/1 by 7/7:

`(1)/(1)* (7)/(7)=(7)/(7)\\\\-(4)/(1)* (7)/(7)=-(28)/(7)\\\\(15)/(7)-(28)/(7)=|(6)/(7)+(7)/(7)|`

Next, solve the addition and subtraction:

`-(13)/(7)=(13)/(7)`

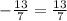
Since -13/7 is not equal to 13/7, this means that 3/7 is an extraneous solution.