First, find the vertices of the shaded region.
x≥0, y≥0 represents the first quadrant.
x + y ≤ 11 has intercepts at (11,0) and (0, 11)
2y ≥ x has intercepts at (0, 0)
x + y ≤ 11 and 2y ≥ x intercept at
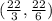
The vertices within the shaded region are (0, 11), (0, 0), and
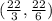 .
.
Next, evaluate the function P = 2x + y at those intercepts.
P = 2x + y at (0, 11) ⇒ P = 2(0) + (11) ⇒ P = 0 + 11 ⇒ P = 11
P = 2x + y at (0, 0) ⇒ P = 2(0) + (0) ⇒ P = 0 + 0 ⇒ P = 0
P = 2x + y at
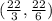 ⇒ P = 2
⇒ P = 2
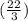 +
+
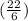 ⇒ P =
⇒ P =
 +
+
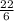 ⇒ P =
⇒ P =
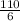 ⇒ P =
⇒ P =
 = 19
= 19

The maximum is found at
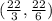
Answer: maximum is 19
