Answer:
![\frac{\sqrt[3]{20}}{5}](https://img.qammunity.org/2022/formulas/mathematics/high-school/kh1bydqrd9ydir1ir5h1dni5gql566367k.png)
Explanation:
Let
![x = \sqrt[3]{(4)/(25)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/l2wb087c5umuc5ee9yib2jukp3cgnq154f.png) , we proceed to show the procedure to determine the simplest form of this number:
, we proceed to show the procedure to determine the simplest form of this number:
1)
![\sqrt[3]{(4)/(25) }](https://img.qammunity.org/2022/formulas/mathematics/high-school/x81oggacqdjm3gm36eir5vkxks6efe1wmb.png) Given.
Given.
2)
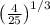 Definition of cubic root.
Definition of cubic root.
3)
![[4\cdot (25)^(-1)]^(1/3)](https://img.qammunity.org/2022/formulas/mathematics/high-school/epd6ep1td04kytjv42yorvdifbeeyosz5s.png) Definition of division.
Definition of division.
4)
![(4)^(1/3)\cdot [(25)^(-1)]^(1/3)](https://img.qammunity.org/2022/formulas/mathematics/high-school/lsj0rokrrm65pmp940zkk92n9wtkrlcoh9.png)
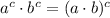
5)
![\{(4)^(1/3)\cdot [(25)^(-1)]^(1/3)\} \cdot \{[(25)^(-1)]^(2/3)\cdot [(25)^(-1)]^(-2/3)\}](https://img.qammunity.org/2022/formulas/mathematics/high-school/bpssvejcgm2xdavesgka257ibvn88crqph.png) Modulative and associative properties/Existence of multiplicative inverse/
Modulative and associative properties/Existence of multiplicative inverse/
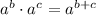
6)
![\{(4)^(1/3)\cdot [(25)^(-1)]^(-2/3)\}\cdot \{[(25)^(-1)]^(1/3)\cdot [(25)^(-1)]^(2/3)\}](https://img.qammunity.org/2022/formulas/mathematics/high-school/24l4wslwy489mehrap8nsbyibg26j2gdti.png) Commutative and associative properties
Commutative and associative properties
7)
![\{(4)^(1/3)\cdot [(25)^(-1)]^(-2/3)\}\cdot (25)^(-1)](https://img.qammunity.org/2022/formulas/mathematics/high-school/j0or2jjqztzgxcndb3h7e6arbtnxg6bg7c.png)
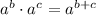
8)
![[(4)^(1/3)\cdot (25)^(2/3)]\cdot (25)^(-1)](https://img.qammunity.org/2022/formulas/mathematics/high-school/nyqnh28l6pdd1bjqli6chst296sgadcq3c.png)
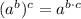
9)
![[4\cdot (25)^(2)]^(1/3)\cdot (25)^(-1)](https://img.qammunity.org/2022/formulas/mathematics/high-school/3825h2k9iyvrpphu36ngk8ze0pa8criisb.png)
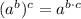 /
/
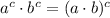
10)
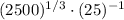 Definition of power and multiplication.
Definition of power and multiplication.
11)
![[(125)\cdot (20)]^(1/3)\cdot (25)^(-1)](https://img.qammunity.org/2022/formulas/mathematics/high-school/7dq116g0ynspgeid9mw8cpcgbp9zuj7376.png) Definition of multiplication.
Definition of multiplication.
12)
![(125)^(1/3)\cdot [(20)^(1/3)\cdot (25)^(-1)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/x4ae1wmco4rqi60z6dqsz5uv1mq6ca5ukt.png)
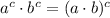 /Associative property.
/Associative property.
13)
![5\cdot [(20)^(1/3)\cdot (25)^(-1)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/5mvmjuenfgcmf4qaczfnckb176b106dpnv.png) Definition of cubic root.
Definition of cubic root.
14)
![5\cdot [(20)^(1/3)\cdot (5)^(-1)\cdot (5)^(-1)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/30l7ebifh8l0ad8ptkxy3aq2sg32ym08rq.png) Definition of multiplication/
Definition of multiplication/
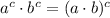
15)
![[(20)^(1/3)\cdot (5)^(-1)][5\cdot (5)^(-1)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/iopo2kmjg5inkry1sky1g4dt3o5m78bzn7.png) Commutative and associative properties.
Commutative and associative properties.
16)
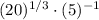 Existence of multiplicative inverse/Modulative property
Existence of multiplicative inverse/Modulative property
17)
![\frac{\sqrt[3]{20}}{5}](https://img.qammunity.org/2022/formulas/mathematics/high-school/kh1bydqrd9ydir1ir5h1dni5gql566367k.png) Definitions of cubic root and division/Result
Definitions of cubic root and division/Result