Answer:
a) Cartesian coordinates of (2.50 m, 30.0°) = (2.17.1.25)
Cartesian coordinates of (3.80 m, 120.0°) = (-1.90.3.29)
b) Distance between (2.17.1.25) and (-1.90.3.29) = 4.55 meter.
Step-by-step explanation:
Points in polar coordinates = (2.50 m, 30.0°) and (3.80 m, 120.0°)
(2.50 m, 30.0°) = (2.50*cos 30, 2.50*sin 30) = (2.17.1.25)
(3.80 m, 120.0°) = (3.80*cos 120, 3.80*sin 120) = (-1.90.3.29)
a) Cartesian coordinates of (2.50 m, 30.0°) = (2.17.1.25)
Cartesian coordinates of (3.80 m, 120.0°) = (-1.90.3.29)
b) We have distance between (a,b) and (c,d) by distance formula
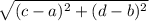
So distance between (2.17.1.25) and (-1.90.3.29) =

Distance between (2.17.1.25) and (-1.90.3.29) = 4.55 meter.