Question

A student places an object with a mass of m on a disk at a position r from the center of the disk. The student starts rotating the disk. When the disk reaches a speed of 0.8 m/s, the object starts to slide off the disk. What is the coefficient of static friction between the object and the disk?

mass=100 g, r= 0.75 m​

Answer 1

The coefficient of static friction between the object and the disk is 0.087.

Step-by-step explanation:

According to the statement, the object on the disk experiments a centrifugal force due to static friction. From 2nd Newton's Law, we can represent the object by the following formula:

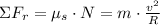`\Sigma F_(r) = \mu_(s)\cdot N = m\cdot (v^(2))/(R)` (1)

`\Sigma F_(y) = N - m\cdot g = 0` (2)

Where:

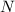`N` - Normal force from the ground on the object, measured in newtons.

`m` - Mass of the object, measured in newtons.

`g` - Gravitational acceleration, measured in meters per square second.

`v` - Linear speed of rotation of the disk, measured in meters per second.

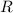`R` - Distance of the object from the center of the disk, measured in meters.

By applying (2) on (1), we obtain the following formula:

`\mu_(s)\cdot m\cdot g = m\cdot (v^(2))/(R)`

`\mu_(s) = (v^(2))/(g\cdot R)`

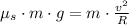
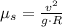
If we know that
`v = 0.8\,(m)/(s)`,
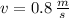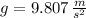`g = 9.807\,(m)/(s^(2))` and
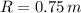`R = 0.75\,m`, then the coefficient of static friction between the object and the disk is:

`\mu_(s) = (\left(0.8\,(m)/(s) \right)^(2))/(\left(9.807\,(m)/(s^(2)) \right)\cdot (0.75\,m))`

`\mu_(s) = 0.087`

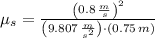
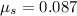
The coefficient of static friction between the object and the disk is 0.087.