Answer :
Partial pressure of
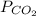 = 639.952 mmHg
= 639.952 mmHg
Partial pressure of
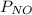 = 36.757 mmHg
= 36.757 mmHg
Partial pressure of
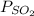 = 5.757 mmHg
= 5.757 mmHg
Partial pressure of
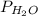 = 69.533 mmHg
= 69.533 mmHg
Solution : Given,
Total pressure,
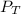 = 752 mmHg
= 752 mmHg
From the periodic table, the molar masses of
 , NO,
, NO,
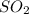 and
and
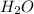 are 44, 30, 64, 18 respectively.
are 44, 30, 64, 18 respectively.
92%
 by mass means 92g
by mass means 92g
 is present in 100g of smoke.
is present in 100g of smoke.
3.6% NO by mass means 3.6g NO is present in 100g of smoke.
1.2%
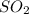 by mass means 1.2g
by mass means 1.2g
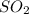 is present in 100g of smoke.
is present in 100g of smoke.
4.1%
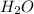 by mass means 4.1g
by mass means 4.1g
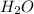 is present in 100g of smoke.
is present in 100g of smoke.
step 1 : First calculate the number of moles of each gas.
Formula used :
Number of moles =
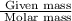 ........(1)
........(1)
Moles of
 ,
,
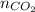 =
=
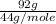 = 2.09 moles
= 2.09 moles
Moles of NO,
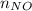 =
=
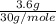 = 0.12 moles
= 0.12 moles
Moles of
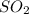 ,
,
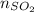 =
=
 = 0.018 moles
= 0.018 moles
Moles of
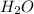 ,
,
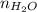 =
=
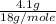 = 0.227 moles
= 0.227 moles
Total number of moles,
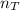 is calculated as
is calculated as
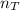 =
=
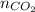 +
+
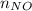 +
+
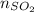 +
+
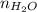 = 2.09 + 0.12 + 0.018 + 0.227 = 2.455 moles
= 2.09 + 0.12 + 0.018 + 0.227 = 2.455 moles
step 2 : Now calculate the partial pressure of each gas.
Formula used :
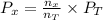 .........(2)
.........(2)
where,
 = partial pressure of x
= partial pressure of x
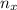 = moles of x
= moles of x
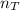 = total moles
= total moles
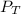 = total pressure
= total pressure
Now put all the values in above formula (2), we get
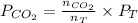 =
=
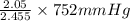 = 639.952 mmHg
= 639.952 mmHg
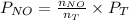 =
=
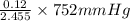 = 36.757 mmHg
= 36.757 mmHg
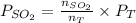 =
=
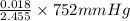 = 5.5136 mmHg
= 5.5136 mmHg
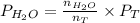 =
=
 = 69.533 mmHg
= 69.533 mmHg