solution:
Let X and Y be two rational numbers. By definition, X and Y can be written as a quotient of two integers.
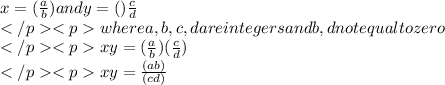
Integers are closed under multiplication. That is, the product of any two integers is an integer. Therefore, ab is an integer and cd is an integer. Thus, XY is written as a quotient of two integers. Therefore, by definition of a rational number, XY is rational.