Question

Two students are on a balcony 19.6 m above the street. one student throws a ball vertically downward at 14.7 m/s; at the same instant, the other student throws a ball ver- problems 53 tically upward at the same speed. the second ball just misses the balcony on the way down. (a) what is the difference in the two ballsâ time in the air? (b) what is the velocity of each ball as it strikes the ground? (c) h

Answer 1

a) Time difference in ball hitting ground in 2 cases = 3 seconds.

b) Velocity of both balls hitting ground is same, which is equal to 24.5 m/s.

Step-by-step explanation:

We have equation of motion ,
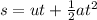`s= ut+(1)/(2) at^2`, s is the displacement, u is the initial velocity, a is the acceleration and t is the time.

a) Let the upward direction be negative and downward direction be positive. Now considering the case where student throws downward.

We have u = 14.7 m/s, acceleration = acceleration due to gravity = 9.8
`m/s^2`, we need to find time when s = 19.6 m.

`19.6=14.7*t+(1)/(2) *9.8*t^2\\ \\ t^2+3t-4=0\\ \\ (t-1)(t+4)=0`

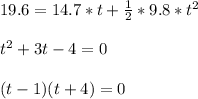
So we will get t = 1 seconds or t = -4 seconds(not possible)

So ball reaches ground after 1 second when thrown downward with velocity 14.7 m/s.

Now considering the case where student throws downward.

We have u = -14.7 m/s, acceleration = acceleration due to gravity = 9.8
`m/s^2`, we need to find time when s = 19.6 m.

`19.6=-14.7*t+(1)/(2) *9.8*t^2\\ \\ t^2-3t-4=0\\ \\ (t+1)(t-4)=0`

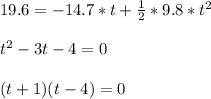
So we will get t = 4 seconds or t = -1 seconds(not possible)

So ball reaches ground after 4 second when thrown upward with velocity 14.7 m/s.

Time difference = 4 - 1 = 3 seconds.

b) We have equation of motion, v = u + at, where v is the final velocity, u is the initial velocity, a is the acceleration and t is the time taken.

Now considering the case where student throws downward.

We have u = 14.7 m/s, acceleration = acceleration due to gravity = 9.8
`m/s^2`, and t = 1 second.

v = 14.7 + 9.8 * 1 = 24.5 m/s

So ball thrown downward with velocity 14.7 m/s strikes ground at 24.5 m/s.

Now considering the case where student throws downward.

We have u = -14.7 m/s, acceleration = acceleration due to gravity = 9.8
`m/s^2`, and t = 4 second.

v = -14.7 + 9.8 * 4 = 24.5 m/s

So ball thrown upward with velocity 14.7 m/s strikes ground at 24.5 m/s.