Answer:
1)
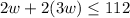
2)
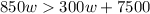
3) The greatest age that Sue could be is 7.
4) The smaller of the two integers is 92.
5) Don needs to earn at least 244 points in the fourth game.
Explanation:
1) An rectangle has 2 dimensions: width(w) and length(l)
The perimeter P is:

The problem states that the length of a rectangle is three times its width. So l = 3w and:
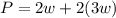
The perimeter of the rectangle is at most 112 cm. It means that the perimeter can be 112, so the equal sign enters the inequality. So
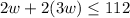
2)
The problem states that he earns $850 per week in sales. His earnings is modeled by the following equation:
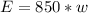 , in which w is the number of weeks.
, in which w is the number of weeks.
The problem also states that he spent $7500 to obtain his merchandise, and it costs him $300 per week for general expenses. So his expenses can be modeled by the following equation
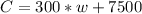 , in which w is also the number of weeks.
, in which w is also the number of weeks.
He will make a profit when his earnings are bigger than his expenses, so: When they are equal, there is no profit, so the equal sign does not enter the inequality.
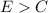
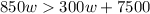
3)
I am going to call Jenny's age x and Sue's age y.
The problem states that Jenny is eight years older than twice her cousin Sue’s age. So
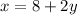 .
.
The sum of their ages is less than 32, so:
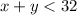
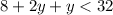

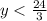
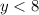
Sue's age has to be less than 8, so the greatest age that Sue could be is 7.
4)
The sum of two consecutive integers is at least 185.
There are two integers with sum of 185, so:
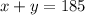
They are consecutive so:
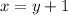
Replacing in the sum equation:
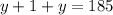


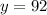
The smaller of the two integers is 92.
5)
The average is the sum of all the scores divided by the number of games. So:
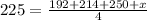
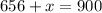
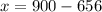
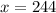
Don needs to earn at least 244 points in the fourth game.