Let us consider two bodies having masses m and m' respectively.
Let they are separated by a distance of r from each other.
As per the Newtons law of gravitation ,the gravitational force between two bodies is given as -
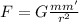 where G is the gravitational force constant.
where G is the gravitational force constant.
From the above we see that F ∝ mm' and
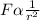
Let the orbital radius of planet A is
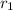 = r and mass of planet is
= r and mass of planet is
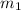 .
.
Let the mass of central star is m .
Hence the gravitational force for planet A is
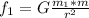
For planet B the orbital radius
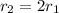 and mass
and mass
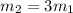
Hence the gravitational force
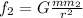
![f_(2) =G(m*3m_(1) )/([2r_(1)] ^(2) )](https://img.qammunity.org/2019/formulas/physics/college/p0ciyz4dwhfx4e3nhwo37w9ucos4jm5kxz.png)

Hence the ratio is
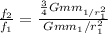
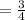 [ ans]
[ ans]