Question

Evaluate cot 120° without using a calculator by using ratios in a reference triangle.

Answer 1

The value of cot 120° is
`-(√(3))/(3)`.

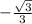Explanation:

Consider the trigonometric identity:

`cot(180-\theta)= -cot(\theta)`

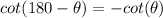
Now use the above trigonometric identity:

`cot(120)= cot(180-60)`

`cot(180-60)= -cot(60)`

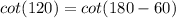
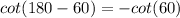
Now use the identity:
`cot(\theta)=(1)/(tan(\theta))`

`-cot(60)=-(1)/(tan(60))`

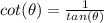
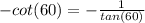
Substitute the value of tan 60°.

`-(1)/(tan(60))=-(1)/(√(3))`

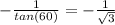
Now rationalize the denominator gives us:

`-(√(3))/(3)`

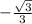
Hence, the value of cot 120° is
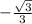`-(√(3))/(3)`.

Answer 2

The reference angle for
`120\degree` is
`60\degree`.

Recall that
`cot(120\degree) = (1)/(tan(120\degree))`

This implies that
`cot(120\degree) = (1)/(tan(60\degree))`

Recall also from
`30\degree - 60\degreee - 90\degree` triangle that


`tan(60\degree)=\sqrt(3)` and also since
`120\degree` is the in the second quadrant, the tangent ratio is negative.

Putting all together we have


`cot(120\degree) = (1)/(-\sqrt(3))`

Rationalizing the denominator gives


`cot(120\degree) = (-\sqrt(3))/(3)`