Answer:
H in terms of c is H = 5c³.
Explanation:
Given that:
H = 40 and c = 2
H varies directly to the cube of c.
Which means that,
H ∝ c³
Let,
k be the proportionality constant.
H = kc³
Putting H=40 and c=2

Dividing both sides by 8,
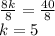
Now,
H in terms of c.
H = 5c³
Hence,
H in terms of c is H = 5c³.