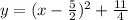Question

how do you rewrite : y=x^2-5x+9 in standard form using complying the square? I keep getting to : x^2-5x-25/4 but I’m not allowed to use a calculator so how do I factor that??

Answer 1

I presume with this you meant to say you want this equation in general form, also known as vertex form, which is y = a(x - h)² + k, instead of standard form, which is y = ax² + bx + c, which is what the original equation is already in.

So with completing the square, you first have to isolate the x-terms. To do this, subtract 9 on both sides of the equation:

`y-9=x^2-5x`

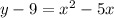
Next, we want to make the right side of the equation a perfect square. To find the constant of this soon-to-be perfect square, divide the x-coefficient by 2 and square that quotient. In this case:

`-5/ 2 = -(5)/(2)\\\\(-(5)/(2))^2=-(5)/(2)*-(5)/(2)=(25)/(4)`

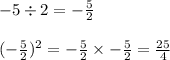
Now add 25/4 on both sides of the equation:

`y-9+(25)/(4)=x^2-5x+(25)/(4)`

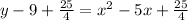
Now to combine -9/1 and 25/4, they must have the same denominator, and to find it you must find the LCD, or lowest common denominator, of 1 and 4. To find it, list the multiples of both and the lowest one they share is their LCD. In this case, the LCD is 4. Multiply both sides of -9/1 by 4/4 and then add the numerators up:

`-(9)/(1)* (4)/(4)=-(36)/(4)\\\\-(36)/(4)+(25)/(4)=-(11)/(4)\\\\y-(11)/(4)=x^2-5x+(25)/(4)`

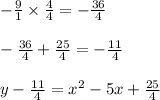
Next, we need to factor the right side of the equation. Using this format of
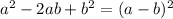`a^2-2ab+b^2=(a-b)^2` , we can factor it as:

`y-(11)/(4)=(x-(5)/(2))^2`

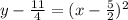
Now lastly, add both sides by 11/4, and your final answer will be
`y=(x-(5)/(2))^2+(11)/(4)`