Question

Let f (x)=1/x and g (x)=x^2+5x. A. Find (f×g)(x). B. Find the domain and range of (f×g)(x).

Answer 1

we are given

`f(x)=(1)/(x)`

`g(x)=x^2+5x`

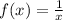
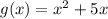
(A)

(f×g)(x)=f(x)*g(x)

now, we can plug it

`(fXg)(x)=(1)/(x) (x^2+5x)`

we can simplify it

`(fXg)(x)=(1)/(x) (x(x+5))`

`(fXg)(x)=x+5`

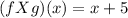
(B)

Domain:

Firstly, we will find domain of f(x) , g(x) and (fxg)(x)

and then we can find common domain

Domain of f(x):

`f(x)=(1)/(x)`

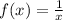
we know that f(x) is undefined at x=0

so, domain will be

`(-\infty,0)`∪
`(0,\infty)`

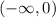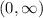
Domain of g(x):

`g(x)=x^2+5x`

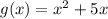
Since, it is polynomial

so, it is defined for all real values of x

now, we can find common domain

so, domain will be

`(-\infty,0)`∪
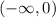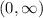`(0,\infty)`..............Answer

Range:

Firstly, we will find range of f(x) , g(x) and (fxg)(x)

and then we can find common range

Range of f(x):

`f(x)=(1)/(x)`

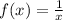
we know that range is all possible values of y for which x is defined

since, horizontal asymptote will be at y=0

so, range is

`(-\infty,0)`∪
`(0,\infty)`

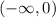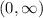
Range of g(x):

`g(x)=x^2+5x`

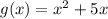
Since, it is quadratic equation

so, its range will be

`[-6.25,\infty)`

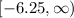
now, we can find common range

so, range will be

`(-6.25,0)`∪
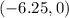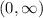`(0,\infty)`.............Answer