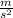Question

help please!! A runner at a speed of 3.5 m/s comes to a stop in 0.15 seconds. What is the deceleration?

Answer 1

Deceleration of the runner is -23.33
`(m)/(s^(2) )`

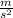
Given:

Initial velocity = 3.5
`(m)/(s)`

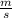
Final velocity = 0
`(m)/(s)`

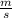
Time = 0.15 s

To find:

Deceleration of runner = ?

Formula used:

According to first equation of motion,

v = u + at

Where, v = final velocity

u = initial velocity

a = deceleration

t = time

Solution:

According to first equation of motion,

v = u + at

Where, v = final velocity

u = initial velocity

a = deceleration

t = time

0 = 3.5 + a (0.15)

-3.5 = 0.15 (a)

a =
`(-3.5)/(0.15)`

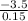
a = -23.33
`(m)/(s^(2) )`

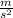
Negative sign shows that it is deceleration.

Thus, deceleration of the runner is -23.33
`(m)/(s^(2) )`