Question

Write a system of equations to model the problem below. Then show the steps to solve your system.

Heather's school is selling tickets to the annual dance competition. On the first day of ticket sales the school sold 6 adult tickets and 7 student tickets for a total of $120. The school took in $168 on the second day by selling 12 adult tickets and 2 student tickets. Find the price of an adult ticket and the price of a student ticket.

Answer 1

Price of adult ticket = x = $13

Price of student ticket = y = $6

Explanation:

Let Price of adult ticket = x

Price of student ticket = y

Now, making equations:

On the first day of ticket sales the school sold 6 adult tickets and 7 student tickets for a total of $120. The equation will be:

`6x+7y=120`

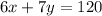
The school took in $168 on the second day by selling 12 adult tickets and 2 student tickets. The equation will be:

`12x+2y=168`

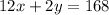
Now, solving the equations simultaneously to find values of x and y.

Let:

`6x+7y=120--eq(1)\\12x+2y=168--eq(2)`

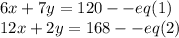
Multiply eq(1) by 12 and then subtract both equations

`12x+14y=240\\12x+2y=168\\-\:\:\:-\:\:\:\:\:\:\:\:\:-\\--------\\12y=72\\y=(72)/(12)\\y=6`

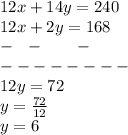
So, we get value of y: y=6

Now, Put value of y in equation 1 to find value of x

`12x+2y=168\\Put\:y=6\\12x+2(6)=168\\12x+12=168\\12x=168-12\\12x=156\\x=(156)/(12)\\x=13`

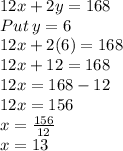
So, we get value of x: x=13

The answer would be:

Price of adult ticket = x = $13

Price of student ticket = y = $6