Answer: C) HF is 4 units and GH is 2 units.
Explanation:
The SSS similarity theorem says that if the side-lengths of the corresponding sides of two triangles are proportional then the triangles are similar.
In ΔDFE and ΔGFH ,
DG = 15, GF = 5, EH = 12, and DE = 8.
To prove ΔDFE and ΔGFH are similar by using SSS similarity theorem we need :-
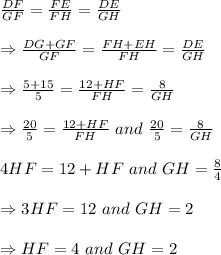
Hence, To prove that △DFE ~ △GFH by the SSS similarity theorem using the information provided in the diagram, it would be enough additional information to know that HF is 4 units and GH is 2 units.