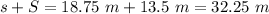Question

A car starts from rest and travels for 5.0 s with a uniform acceleration of +1.5m/s². The driver then applies the brakes, causing a uniform acceleration of -2.0 m/s². if the brakes are applied for 3.0 s, (a) how fast is the car going at the end of the braking period, and (b) how far has the car gone?

Answer 1

Part a)

`v_2 = 1.5 m/s`

Part b)

`d = 39 m`

Step-by-step explanation:

Part a)

Initial speed of the car = 0

acceleration of the car = 1.5 m/s^2

now at the end of t = 5 s the final speed of the car is given as

`v_f - v_i = at`

`v_1 - 0 = (1.5)(5)`

`v_1 = 7.5 m/s`

now after this car apply brakes which produce deceleration

so we have

`a = -2 m/s^2`

time to during which deceleration is applied is given by

`t = 3.0 s`

now we have

`v_f - v_i = at`

`v_2 - 7.5 = (-2)(3)`

`v_2 = 7.5 - 6 = 1.5 m/s`

Part b)

distance moved by car during the period of acceleration of the car is given as

`d = ((v_f + v_i)/(2))(time)`

`d_1 = ((0 + 7.5)/(2))(5)`

`d_1 = 18.75 m`

Now while car is decelerating then the distance moved by the car is given as

`d_2 = ((7.5 + 1.5)/(2))(3)`

`d_2 = 13.5 m`

now total distance moved by the car

`d = d_1 + d_2`

`d = 18.75 + 13.5`

`d = 32.25 m`

Answer 2

We use the equation of motions,

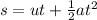`s=ut+(1)/(2)at^2` (A)

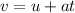`v=u+at` (B)

since a car starts from rest and travels for 5.0 s with a uniform acceleration of +1.5 m/s². therefore the distance traveled by the car for 5 s, from equation (A)

`s=0* 5.0\s+(1)/(2)* 1.5 m/s^2 * (5.0\ s)^2 =18.75\ m`.

Now at the end of 5 s, the velocity of the car from (B),

`v=0+1.5* 5 =7.5\ m/s`.

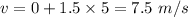After the driver applied the brakes, the distance traveled by the car, again from equation (A)

`S=7.5* 3.0s+(1)/(2) (-2.0 m/s^2)(3)^2=13.5\ m`.

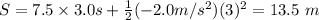At the end of the brakes applied, the velocity

`V=7.5+(-2\ m/s^2)*3=15\ m/s.`.

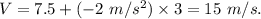The total distance traveled by the car,

`s+S=18.75\ m+13.5\ m=32.25\ m`