Question

The coordinates of the vertices of​ quadrilateral ABCD ​ are A(−4, −1) , B(−1, 2) , C(5, 1) , and D(1, −3) .

Drag and drop the choices into each box to correctly complete the sentences.

Answer 1

Hi there, KawallPotato! :)

Finding the slope of a line is finding the rise over run, or the change in y over the change in x. Let me show you what I mean.

Slope = change in y / change in x

Or in other words,
`(y2 - y1)/(x2 - x1)`

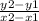
Let's try it with AB. The first thing to consider is the placement of the letters. The blank space is asking for the slope of point A to point B, which means that the coordinates of A are your y₁ and x₁ values and the coordinates of B are your y₂ and x₂ values.

Put them in the equation like this:

`(2 - (-1))/(-1 - (-4))`

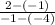
2 - (-1) is a double negative, so it becomes 2 + 1, which is 3.

-1 - (-4) turns into -1 + 4 for the same reason. The change in x is also 3.

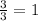`(3)/(3) = 1`, so the slope of line AB is 1.

Using the same method, we can solve the next three problems.

Coordinates of B: (-1, 2)

Coordinates of C: (5, 1)

Slope:
`(1 - 2)/(5 - (-1)) = (-1)/(5+1) = -(1)/(6)`

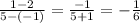
The slope of BC is -1/6.

Coordinates of C: (5, 1)

Coordinates of D: (1, -3)

Slope:
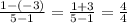`(1 - (-3))/(5 - 1) = (1 + 3)/(5 -1) = (4)/(4)`, so the slope is 1.

Coordinates of A: (-4, -1)

Coordinates of D: (1, -3)

Slope:
`(-1 - (-3))/(1 - (-4)) =  -(2)/(5)`

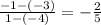
The slope is
`-(2)/(5)`.

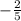Quadrilateral
`ABCD` is not a parallelogram because it has only one pair of parallel opposite sides.

I hope this was helpful. Have a great day. :D