Question

The coordinates of the vertices of △ABC are A(−2,2), B(5,−3), and C(−4,−1). Identify the perimeter of △ABC. Round each side length to the nearest tenth before adding. HELP PLEASE!

Answers:
21.4
30.9
10.7

Answer 1

the distance from (-2,2) to (5,-3) is 8.6,

(5,-3) to (-4,-1) is 9.2

(-4,-1) to (-2,2) is 3.6

8.6+9.2+3.6= 21.4

so the perimeter is 21.4

Answer 2

21.4

Explanation:

Given: The coordinates of the vertices of △ABC are A(−2,2), B(5,−3), and C(−4,−1).

To find: Identify the perimeter of △ABC. Round each side length to the nearest tenth.

Solution: To find the perimeter of △ABC, we first need to find the length AB, BC and AC.

We know the distance formula between the coordinates
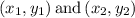`\left ( x_(1),y_(1) \right ) \text{and} \left ( x_(2),y_(2) \right )` is
`\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`

`AB=\sqrt{(5+2)^(2) +(-3-2)^(2) } =√(49+25)=√(74)=8.60`

`BC=\sqrt{(-4-5)^(2) +(-1+3)^(2) } =√(81+4)=√(85)=9.21`

`AC=\sqrt{(-4+2)^(2) +(-1-2)^(2) } =√(4+9)=√(13)=3.60`

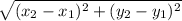
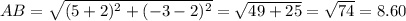
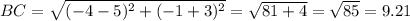
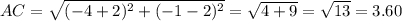
Now, rounding each side to the nearest tenth we have,

`AB=8.6`

`BC=9.2`

`AC=3.6`

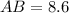
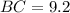
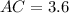
Now, perimeter of △ABC
`=AB+BC+AC`

`=8.6+9.2+3.6`

`=21.4`

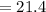
Hence, perimeter of △ABC is 21.4.