Question

1. Calculate the length of the space diagonal of a block with dimensions:

W = 5 cm, 1 = 8 cm, h = 12 cm.
Round to the nearest tenth. T
l
V12 +w? th?
15.2 cm
15.3 cm
12.6 cm
12.3 cm

Answer 1

Given:

Dimensions of a block are w = 5 cm, l = 8 cm, h = 12 cm.

To find:

The length of the space diagonal of a block.

Solution:

Length of the diagonal is

`Diagonal=√(l^2+w^2+h^2)`

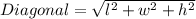
Putting the given values, we get

`Diagonal=√((8)^2+(5)^2+(12)^2)`

`Diagonal=√(64+25+144)`

`Diagonal=√(233)`

`Diagonal=15.2643375...`

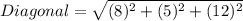
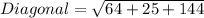
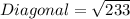
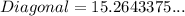
Round to the nearest tenth.

`Diagonal\approx 15.3`

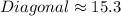
So, the length of the space diagonal of a block is 15.3 cm.

Therefore, the correct option is B.