Question

Find the domain for the function f(x) = the quotient of the square root of the quantity x minus 3 and the quantity x minus 5.

Answer 1

f(x) = sqrt [( x - 3) / (x - 5)]

well x cannot be 5 because that would make x - 5 = 0.

Also the fraction x - 3 / x - 5 cannot be negative because theres no real square root of a negative.

So x must be <= 3 or > 5

In interval notation the domain is ( -∞,3] or (5 , ∞)

Answer 2

The domain is (-∞, 3] and (5, ∞)

Explanation:

The given function is
`\sqrt{(x -3)/(x - 5) }`

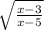
In order to find the domain, the denominator cannot be zero and quotient must not be a negative number.

Here the denominator is x - 5

Which must be greater than zero.

x - 5 > 0

x > 5

The numerator must be less than or equal to 0.

x - 3 ≤ 0

x ≤ 3

Therefore, the domain is (-∞, 3] and (5, ∞)