Question

The Hot Summer Fair is coming to town! Admission to the fair costs $12.99 and each ride costs $1.75. You have $35 to spend at the fair including admission.

Part A: Write an inequality that represents this situation.


Part B: Solve the inequality to determine the maximum number of rides you can enjoy at the Hot Summer Fair.


(Please help me! I think I understand but I am not 100% sure.)

Answer 1

The required inequality is
`12.99+1.75x\leq 35`.

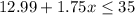You can ride maximum 12 rides.

Explanation:

Consider the provided information.

Part(A)

Admission to the fair costs $12.99 and each ride costs $1.75.

Let you rides x number of rides.

Thus the expression for the total cost will be:

`12.99+1.75x`

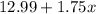
It is given that you have $35 to spend at the fair including admission.

That means you can pay $35 or less than it. So the required inequality is:

`12.99+1.75x\leq 35`

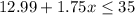
Thus, the required inequality is
`12.99+1.75x\leq 35`.

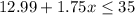Part(A) Now we need to find the maximum number of rides you can enjoy at the Hot Summer Fair.

Solve the inequity for x as shown:

`12.99+1.75x\leq 35`

`1.75x\leq 35-12.99`

`1.75x\leq 22.01`

`x\leq (22.01)/(1.75)`

`x\leq 12.58`

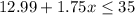
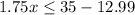
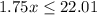
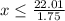
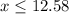
Thus, the number of ride should be less than or equal to 12.

Hence, you can ride maximum 12 rides.

Answer 2

As given,

Admission to the fair costs = $12.99

Cost of each ride = $1.75

Total money present = $35

Let the number of rides a person can take be x

Part A: The inequality that represents this situation is

35≤ 12.99 + x(1.75) where x represent the number of rides a person can take.

Part B:

Solving the equation we get,

35 = 12.99 + x(1.75)

1.75x = 35-12.99

1.75x = 22.01

x =
`(22.01)/(1.75)`

x = 12.577

Hence a person can take upto 12 rides.