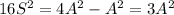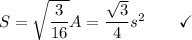Question

using the Pythagorean thereom, find the are of an equilateral triangle whose sides measure 5 units. Find the are to the nearest tenth of a square unit.

Answer 1

An equilateral triangle isn't a right triangle, so the Pythagorean Theorem doesn't apply directly.

But if we divide an equilateral triangle with side s in half along an altitude, we get two congruent right triangles each with hypotenuse s and one leg s/2.

The other leg is the altitude h we divided along. By the Pythagorean Theorem

`( \frac s 2)^2 + h^2 = s^2`

`(s^2)/(4) + h^2 = s^2`

`h^2 = (3)/(4) s^2`

`h = (√(3))/(2) s`

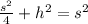
The area A of our original equilateral triangle is now

`A= \frac 1 2 sh = \frac 1 2 s \left( ( √(3))/(2) s \right) = (√(3))/(4) s^2`

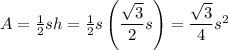
So the area of our equilateral triangle of side 5 is

`A = (√(3))/(4) (5)^2 = (25)/(4) √(3) \approx 10.8`

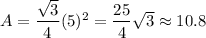
Answer: 10.8

I don't like ruining a nice exact answer with an approximation, but the question asks for one.

We could have done the above steps with 5 in particular instead of s but I prefer to do the general solution and substitute at the end.

----

Since you read this far, I will give you the secret formula for the area S of a triangle given squared sides A, B, C. Your teachers won't even know this one.

`16S^2 = 4AB-(A+B-C)^2`

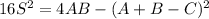
Let's try it out for
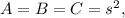`A=B=C=s^2,` an equilateral triangle:

`16S^2 = 4A^2 -A^2 = 3A^2`

`S = \sqrt{(3)/(16)} A = (√(3))/(4) s^2 \qquad\checkmark`