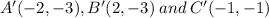The transformation is a reflection in the line
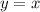
followed by a reflection in the line

.
The mapping for a reflection in the line
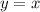
is
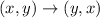
.
That is simply swapping the coordinates.
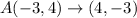
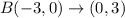
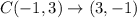
Now we reflect the resulting coordinates in the line

which has the mapping
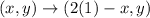
So we transform the resulting coordinates as follows:
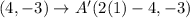
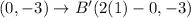
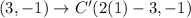
Hence we have