The difference of two squares factoring pattern states that a difference of two squares can be factored as follows:
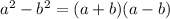
So, whenever you recognize the two terms of a subtraction to be two squares, you can factor it as the sum of the roots multiplied by the difference of the roots.
In this case, the squares are obvious:
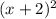 is the square of
is the square of
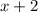 , and
, and
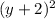 is the square of
is the square of
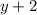
So, we can factor the expression as
![(x+2)^2 - (y+2)^2 = [(x+2)+(y+2)] - [(x+2)+(y+2)]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/anbfwg7o1hemmjbsrxq116imhn2z5uwbpz.png)
(the round parenthesis aren't necessary, I used them only to make clear the two terms)
We can simplify the expression summing like terms:
![(x+2)^2 - (y+2)^2 = [(x+2)+(y+2)][(x+2)-(y+2)] = (x+y+4)(x-y)](https://img.qammunity.org/2019/formulas/mathematics/middle-school/udntwxpwnn5j54irzs5atjncgn620rprjx.png)