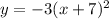we are given
parent function as
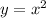
(1)
vertical stretch of factor 2
so, we can multiply y-value by 2
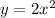
then a shift right of 3 units
so, we can replace x as x-3
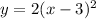
(2)
a shift left by 2 units
we can replace x as x+2
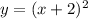
then a horizontal shrink factor of 1/2
so, we can multiply by 2 to x-value
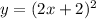
then a shift down of 5 units
we can subtract y-value by 5
so, we get
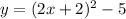
(3)
a shift to the right 1 unit
we can replace x as x-1
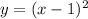
stretched vertically by a factor of 1/2
we can multiply y-value by 1/2
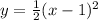
then is shifted down 4 units
we can subtract y-value by 4
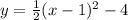
(4)
reflected across the x-axis
we can multiply y-value by -1
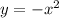
tretched vertically by a factor of 3
multiply y-value by 3
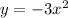
shifted left 7 units
we can replace x as x+7