Question

Ccording to coulomb's law, which pair of charged particles has the lowest potential energy? according to coulomb's law, which pair of charged particles has the lowest potential energy? a particle with a 1− charge separated by 100 pm from a particle with a 3+ charge. a particle with a 1− charge separated by 100 pm from a particle with a 2+ charge. a particle with a 1− charge separated by 200 pm from a particle with a 1+ charge.

Answer 1

Coulombs law says that the force between any two charges depends on the amount of charges and distance between them. This force is directly proportional to the magnitude of the two charges and inversely proportional to the distance between them.

`F=k(|q_1| |q_2|)/(r^2)`

where
`q_1\hspace{1mm}and\hspace{1mm}q_2` are charges,
`r` is the distance between them and k is the coulomb constant.

case 1:

`q_1=-e\\ q_2=+3e\\ r=100pm\\ \Rightarrow F=k(|-e||3e|)/((100pm)^2)=3ke^2*10^8`

case 2

`q_1=-e\\ q_2=+2e\\ r=100pm\\ \Rightarrow F=k(|-e||2e|)/((100pm)^2)=2ke^2*10^8`

case 3:

`q_1=-e\\ q_2=+e\\ r=100pm\\ \Rightarrow F=k(|-e||e|)/((200pm)^2)=0.25ke^2*10^8`

Comparing the 3 cases:

The maximum potential force according to coulombs law is between -1 charge and +3 charge separated by a distance of 100 pm.

Answer 2

Answer: The electrostatic potential energy of a particle with a 1− charge separated by 200 pm from a particle with a 1+ charge.

Explanation:

The formula for the electrostatic potential energy is as follows;

`U=(kq_(1)q_(2))/(r)`

Here, U is the potential energy,
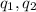`q_(1),q_(2)` are the charges and r is the distance between them.

Here,
`k=(1)/(4\pi(\epsilon _(0)))`

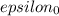`epsilon _(0)` is the absolute permittivity of free space.

Calculate the electrostatic potential energy of a particle with a 1− charge separated by 100 pm from a particle with a 3+ charge.

`U=(kq_(1)q_(2))/(r)`

Put q_{1}=-1, q_{2}=+3,k=
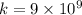`k=9* 10^(9)` and r=100 pm.

`U=(k(1)(3))/(100 pm)`

`U=-k0.03`

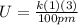
Calculate the electrostatic potential energy of a particle with a 1− charge separated by 100 pm from a particle with a 2+ charge.

`U=(kq_(1)q_(2))/(r)`

Put q_{1}=-1, q_{2}=+2 and r=100 pm.

`U=(k(-1)(+2))/(100 pm)`

`U=-k0.02`

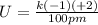
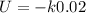
Calculate the electrostatic potential energy of a particle with a 1− charge separated by 200 pm from a particle with a 1+ charge.

`U=(kq_(1)q_(2))/(r)`

Put q_{1}=-1, q_{2}=+1 and r=200 pm.

`U=(k(-1)(+1))/(200 pm)`

`U=-k0.005`

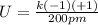
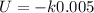
Therefore, the electrostatic potential energy of a particle with a 1− charge separated by 200 pm from a particle with a 1+ charge.