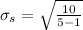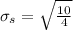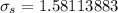Answer: The standard deviation of the sample is 1.58.
We calculate the standard deviation as follows:
Let time taken by employees be t
Let the Mean time (average) taken by employees be
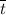
t t -
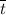 (t -
(t -
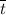 )²
)²
8
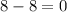
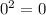
7
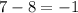
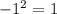
9
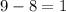
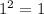
6

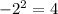
10
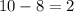
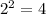
Total 40 10
We find the mean or average as follows:
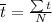
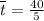

The formula for calculating the standard deviation of a sample is: