Question

The wing color of a certain species of moth is controlled by alleles at a single locus. Gray (G) is dominant to white (g). A scientist studied a large population of these moths, tracking the frequency of the G allele over time, as shown in the figure below: A graph showing the frequency of G allele in a population over 20 years. The frequency in 1960 is 0.8 and decreases to 0.5 by 1980. © 2012 FLVS Assuming that the population was in Hardy-Weinberg equilibrium for this gene, what percentage of the moth population was heterozygous in 1960? 20% 32% 40% 64%

Answer 1

Option B,
`32`%

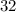Step-by-step explanation:

Given,

Gray (G) is dominant to white (g)

As per Hardy Weinberg's equation, the frequency of dominant allele is represented by "p" and recessive allele is represented by "q"

In 1960, the frequency of allele "G" is
`0.8`

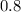
So it means,
`p=0.8`

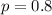
As per Hardy Weinberg's I equilibrium equation-

`p+q=1\\`

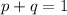
Substituting the value of "p" in above equation, we get -

`q= 1-9\\q=1-0.8\\q=0.2`

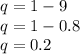
Then, the frequency of population of moth with genotype "GG" is
`p^2`

`p^2= 0.8^2\\p^2= 0.64`

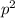
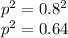
the frequency of population of moth with genotype "gg" is
`q^2`

`q^2= 0.2^2\\q^2= 0.04`

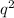
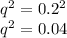
and the frequency of population of moth with heterozygous population with genotype "Gg" is
`2pq`

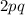
As per Hardy Weinberg's II equilibrium equation-

`p^2+q^2+2pq=1\\`

Substituting the available values in above equation, we get -

`0.64+0.04+2pq=1\\2pq=1-0.04-0.64\\2pq=.32`

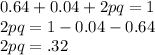
Thus,
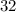`32`% moth population was heterozygous in 1960

Hence, option B is correct

Answer 2

The frequency of allele G (in 1960) is p=0.8

If population is in HW equilibrium than p+q=1, which means that the frequency of the allele q (in 1960) is 0.2.

The frequencies of the genotypes are:

p2=0.64 dominant homozygous

2pq=0.32 heterozygous= 32%

q2=0.04 recessive heterozygous