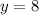The solutions of the system are:
 and
and
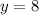
Step-by-step explanation
Given system of equations......
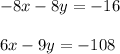
First we need to make the augmented matrix using the given equations....
![\left[\begin{array}{cccc}-8&-8&|&-16\\6&-9&|&-108\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/83267skipooq4rs1qr6xhgvbg34fkh4t9v.png)
Now, we need to transform the augmented matrix to the reduced row echelon form using the row operations.
Row operation 1 : Multiply the 1st row by
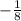 . So, we will get...
. So, we will get...
![\left[\begin{array}{cccc}1&1&|&2\\6&-9&|&-108\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/p0bjfp62djdiat677d0kkjrz1ee3kfyhto.png)
Row operation 2 : Add -6 times the 1st row to the 2nd row. So, we will get...
![\left[\begin{array}{cccc}1&1&|&2\\0&-15&|&-120\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/g2uwdinm0gfd3lj6pfsk2avemzzcyqbbtz.png)
Row operation 3 : Multiply the 2nd row by
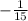 . So, we will get...
. So, we will get...
![\left[\begin{array}{cccc}1&1&|&2\\0&1&|&8\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/u3qcbe4032ugf610auz9bs3m8ufdyc8deb.png)
Row operation 4 : Add -1 times the 2nd row to the 1st row. So, we will get....
![\left[\begin{array}{cccc}1&0&|&-6\\0&1&|&8\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/aczowst647hlrc5uuvlbne5xqx07fodhba.png)
So, this is the reduced row echelon form.
We can get the equations from the above reduced row echelon form as.....
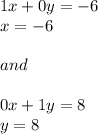
So, the solutions of the system are:
 and
and