Question

An exponential function f(x)

= ab" passes through the points (0, 12000) and (2, 3000). What are the values of a and b ?

Answer 1

Given:

An exponential function
`f(x)=ab^x` passes through the points (0, 12000) and (2, 3000).

To find:

The values of a and b.

Solution:

We have,

`f(x)=ab^x` ...(i)

It passes through the point (0,12000). Putting x=0 and f(x)=12000 in (i), we get

`12000=ab^0`

`12000=a(1)`

`12000=a`

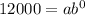
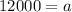
Given function passes through the point (2,3000). Putting x=2, a=12000 and f(x)=3000 in (i), we get

`3000=12000b^2`

`(3000)/(12000)=b^2`

`(1)/(4)=b^2`

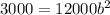
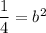
Taking square root on both sides.

`\pm (1)/(2)=b`

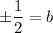
For an exponential function b cannot be negative. So,
`b=(1)/(2)`.

Therefore, the value of a is 12000 and the value of b is
`(1)/(2)`.