Question

B=?
Angle A=?
Angle B=?

Answer 1

1.) Solve for length b.

The simpler method is to use the Pythagorean theorem. If
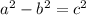`a^2 - b^2 = c^2`, then this means that
`c^2 - a^2 = b^2`.

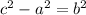Plug in the values:

`11^2 - 7^2 = b^2`

-->
`121 - 49 = 72`

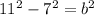
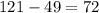
So this means that b is the square root of 72, which is 8.49

2.) Solve for ∠A.

Let's refer to the law of sines. If
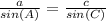`(a)/(sin(A)) = (c)/(sin(C))`, then this means we can cross multiply. Since A is the value we are solving for, the equation should be written out like this:

`A = sin^-1((sin(C) * a)/(c))`

-->
`A = sin^-1((sin(90) * 7)/(11))`

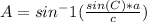
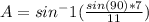
A is 39.52°

3.) Solve for ∠B.

This is the easiest one. The sum of all three angle measures in a triangle add up to 180°. We already know that one of the angles is a right angle and the other 39.52°.

39.52 + 90 = 129.52

180 - 129.52 = 50.48

∠B is 50.48°.