Question

Find the indicated values, where g(t)=t^2-t and f(x)=1+x f(2g(1)

Answer 1

`g(t)=t^2-t\\\\f(x)=1+x\\\\f(2g(1))=?\\\\g(1)=\\_{\text{put t=1 to the equation of g(t)}}\\\\=1^2-1=1-1=0\\---------------\\2g(1)=2(0)=0\\\\f(2g(1))=\\_{\text{put x-0 to the equation of f(x)}}\\\\=1+0=1\\\\Answer:\ f(2g(1))=1`

Answer 2

The indicated value f(2g(1)) is: 1

Explanation:

We are given two functions f(x) in terms of variable 'x' and g(t) in terms of variable 't' as:

`g(t)=t^2-t`

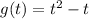
and
`f(x)=1+x`

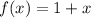
Now we are asked to find the value of the composite function:

`f(2g(1))`

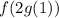
We know that:

`g(1)=1^2-1\\\\g(1)=0`

Hence,

`f(2g(1))=f(2* 0)=f(0)\\\\\\f(0)=1+0\\\\\\f(0)=1`

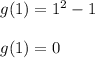
Hence, the indicated value is:

1