Question

I need help using the distance formula to find the perimeter of a parallelogram JKLM

Answer 1

let's first notice the distance of LM, is a vertical line, so we can just do a plain subtraction, -1.6 -(-0.4) => -1.6 +0.4 => -1.2 and the distance is just |-1.2| or 1.2.

let's check KJ, another vertica line, -1.7 - (-0.5) => -1.7 + 0.5 => -1.2 => |-1.2| = > 1.2.

so LM = KJ, and both are vertical, meaning we have a parallelogram, which means KL = JM.

so let's just find say... KL and her twin will be the same.

`\bf ~~~~~~~~~~~~\textit{distance between 2 points} \\\\ K(\stackrel{x_1}{-0.5}~,~\stackrel{y_1}{-1.7})\qquad L(\stackrel{x_2}{-0.7}~,~\stackrel{y_2}{-0.4})~\hspace{3.5em} d = √(( x_2- x_1)^2 + ( y_2- y_1)^2)`

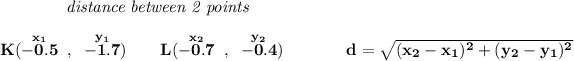
`\bf KL=√([-0.7-(-0.5)]^2+[-0.4-(-1.7)]^2) \\\\\\ KL=√((-0.7+0.5)^2+(-0.4+1.7)^2)\implies KL=√((-0.2)^2+1.3^2) \\\\\\ KL=√(0.04+1.69)\implies KL=√(1.73)\implies KL\approx 1.315 \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ \stackrel{\textit{perimeter}}{\stackrel{LM}{1.2}+\stackrel{KJ}{1.2}+\stackrel{KL}{1.315}+\stackrel{JM}{1.315}}\implies 5.03`