Question

What is the area of a trapezoid ABCD with bases AB and CD , if: m∠C=m∠D=60°, AB = BC = 8 cm

Answer 1

The answer is 83.1384cm²

I wrote a solution but was told that my answer either contains a link or inappropriate words.

I had not included any link or appropriate words.

Answer 2

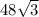`48√(3)` cm².

Explanation:

Given information: Trapezoid ABCD with bases AB and CD, m∠C=m∠D=60°, AB = BC = 8 cm.

m∠C=m∠D=, two base angles are same. It means ABCD is an isosceles trapezoid.

Draw perpendiculars from A and B on side CD. Both triangles ADE and BCF are congruent.

In a right angled triangle,

`\cos \theta =(adjacent)/(hypotenuse)`

`\sin \theta =(opposite)/(hypotenuse)`

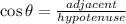
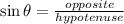
In triangle ADE,

`\cos 60 =(DE)/(AD)`

`(1)/(2)=(DE)/(8)`

`(8)/(2)=DE`

`4=DE`

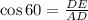
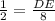
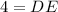
The value of DE is 4.

`\sin 60 =(AE)/(AD)`

`(√(3))/(2) =(AE)/(8)`

`(8√(3))/(2) =AE`

`4√(3)=AE`

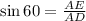
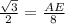
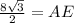
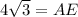
The height of the trapezoid is
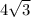`4√(3)`. The length of base DC is

`DC=DE+EF+FC`

`DC=4+8+4=16`

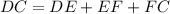
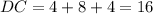
The area of a trapezoid is

`A=(a+b)/(2)* h`

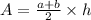
where, a and b are bases of the trapezoid.

`A=(8+16)/(2)* 4√(3)`

`A=12* 4√(3)`

`A=48√(3)`

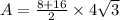
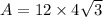
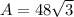
Therefore the area of trapezoid ABCD is
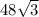`48√(3)` cm².