Formula for arc length is:
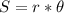 , where
, where
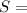 Arc length,
Arc length,
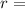 radius of the circle and
radius of the circle and
 central angle in radians.
central angle in radians.
Question 1
The correct option is: 0.67
Step-by-step explanation
Here given that, radius is 15 meter and arc length is 10 meter.
So, plugging
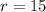 and
and
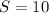 into the above formula......
into the above formula......
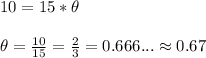
Thus, the central angle of the circle is 0.67 radians.
Question 2
The correct option is: 12.56
Step-by-step explanation
Here, central angle =
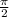 radians and radius = 8
radians and radius = 8
So, plugging
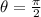 and
and
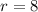 into the formula....
into the formula....
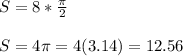
Thus, the length of the arc will be 12.56