Answer:
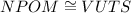 and
and
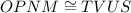 will be correct.
will be correct.
Explanation:
Given: two quadrilaterals having verticals P, N, O,M and S,T,V,U are congruent, where, OM is congruent or equal to TS and
 .
.
in quadrilaterals NPOM and VUTS-
since, the condition
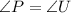
and, side UV=side OM follow for the above quadrilateral. (According to the figure)
then we can say according to the property of quadrilateral, their corresponding sides must be congruent. so they are congruent.
similarly, these two conditions also follow in the case of
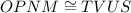
we can understand it by making the figures.