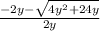Question

Given g(x) =
`(3)/(x^2+2x)` find g^-1(x)

Answer 1

We get:

`g^(-1)(x)=(-x+√(x(x+3)))/(x)\ or\ g^(-1)(x)=(-x-√(x(x+3)))/(x)`

Explanation:

In order to find the inverse of a given function f(x) we follows following steps:

1) Substitute f(x)=y

2) Interchange x and y

3) Solve for y.

Here we have the function g(x) as follows:

`g(x)=(3)/(x^2+2x)`

Now, we substitute:

`g(x)=y`

i.e.

`y=(3)/(x^2+2x)`

Now, we interchange x and y:

`x=(3)/(y^2+2y)\\\\x(y^2+2y)=3\\\\xy^2+2xy-3=0`

We know that the solution to the quadratic equation of the type:

`at^2+bt+c=0`

is given by:

`t=(-b\pm √(b^2-4ac))/(2a)`

Here,

`a=x,\ b=2x\ and\ c=-3`

Hence, the solution is:

`y=(-2x\pm √((2x)^2-4* x* (-3)))/(2* x)\\\\y=(-2x\pm √(4x^2+12x))/(2x)\\\\y=(-2x\pm 2√(x^2+3x))/(2x)\\\\y=(-x\pm √(x^2+3x))/(x)`

i.e.

`y=(-x+√(x(x+3)))/(x),\ y=(-x-√(x(x+3)))/(x)`

Answer 2

We know that g(x) = \frac{3}{x^2+2x}

We have to find g^-1(x) or inverse of g(x)

Inverse of g(x) can be determined by equating g(x) to y, and determining the value of x in terms of y

g(x) = y = \frac{3}{x^2+2x}

⇒ y × (x² + 2x) = 3

⇒ yx² + 2xy = 3

⇒ yx² + 2yx - 3 = 0

Determining the roots of x using:

x =
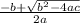`\frac{-b + \sqrt{b^(2) - 4ac}}{2a}` OR x =
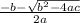`\frac{-b - \sqrt{b^(2) - 4ac}}{2a}` , where a is coefficient of x², b is coefficient of x, and c is the constant

⇒ x =
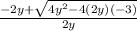`(-2y + √(4y^2 - 4(2y)(-3)))/(2y)` OR x =
`(-2y - √(4y^2 - 4(2y)(-3)))/(2y)`

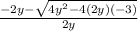
⇒ x =
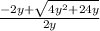`(-2y + √(4y^2 + 24y))/(2y)` OR x =
`(-2y - √(4y^2 + 24y))/(2y)`

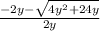
Hence, g^-1(x) =
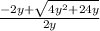`(-2y + √(4y^2 + 24y))/(2y)` OR x =
`(-2y - √(4y^2 + 24y))/(2y)`