Question

Consider the differential equation: (y^2+2*x)dx+(2*x*y-1)dy = 0. (a) show that the equation is exact by evaluating (\partial m)/(\partial y) = (\partial n)/(\partial x)= (b) determine the general solution in implicit form: incorrect: your answer is incorrect. = c

Answer 1

The given ODE

`\underbrace{(y^2+2x)}_M\,\mathrm dx+\underbrace{(2xy-1)}_N\,\mathrm dy=0`

is exact if
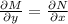`(\partial M)/(\partial y)=(\partial N)/(\partial x)`. It so happens that we have
`(\partial M)/(\partial y)=2y=(\partial N)/(\partial x)`, so it is indeed exact. For such an ODE, we're looking for a solution of the form
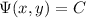`\Psi(x,y)=C`, for which the differential is

`\mathrm d\Psi=(\partial\Psi)/(\partial x)\,\mathrm dx+(\partial\Psi)/(\partial y)\,\mathrm dy=0`

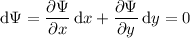
so we have the following system of PDEs that allow us to solve for
`\Psi`:

`(\partial\Psi)/(\partial x)=M=y^2+2x`

`(\partial\Psi)/(\partial y)=N=2xy-1`

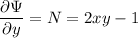
In the first PDE, we can integrate both sides with respect to
`x` and recover
`\Psi`:

`\displaystyle\int(\partial\Psi)/(\partial x)\,\mathrm dx=\int(y^2+2x)\,\mathrm dx`

`\implies\Psi(x,y)=xy^2+x^2+f(y)`

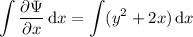
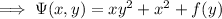
Then differentiating this with respect to
`y` returns
`N`:

`(\partial\Psi)/(\partial y)=2xy+(\mathrm df)/(\mathrm dy)=2xy-1`

`\implies(\mathrm df)/(\mathrm dy)=-1`

`\implies f(y)=-y+C`

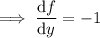
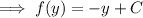
So the general solution to the ODE is

`\Psi(x,y)=xy^2+x^2-y+C=C`

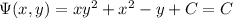
or simply

`xy^2+x^2-y=C`